phototore.blogg.se - The two data curves on the figure illustrate that

#The two data curves on the figure illustrate that how to#
#The two data curves on the figure illustrate that plus#
#The two data curves on the figure illustrate that download#

Because the original standard was 1000 µg/mL, the test sample that produced the same absorbance in the assay also must be 1000 µg/mL. However, the amount of protein per well is almost certainly not the value of interest instead, one usually wants to know the protein concentration of the original test sample. Because there was 10 µg of standard per well, one could report the determined concentration of test sample as 10 µg/well. If the assay results in the test sample having the same final absorbance as the standard sample, then the conclusion is that the test sample contains the same amount of protein as the standard sample. Because 10 µL of the standard sample is added to a well, there is 0.010 mL x 1,000 µg/mL = 10 µg of protein in the well. In the microplate protocol (see figure), one adds 10 µL of sample (test or standard) and 300 µL of assay reagent per well. (Ordinarily, an entire set of standards is necessary to establish a response curve, but this is a simplified example.) 23236) is used to assay two protein samples: a test sample whose concentration is not known, and a standard whose concentration is 1 mg/mL (= 1000 µg/mL).

#The two data curves on the figure illustrate that plus#

Consider a simple example in which the Coomassie Plus Protein Assay Kit (Part No. Contrary to what many people assume, it is neither necessary nor even helpful to know the actual amount (e.g., micrograms) of protein applied to each well or cuvette of the assay.

Loyola University's Center for Science Education has a discussion of the dividing method in this.

Honolulu Community College has a description of the area method and a page on graphs as a part of a Physical Science course.

If you would like to know more about best-fit lines, you can use the links below to read more about them References and resources If you think you have a handle on the construction of a best fit line, click on this bar to try some practice problems with worked answers! Next steps - Some practice problems I am ready to PRACTICE!

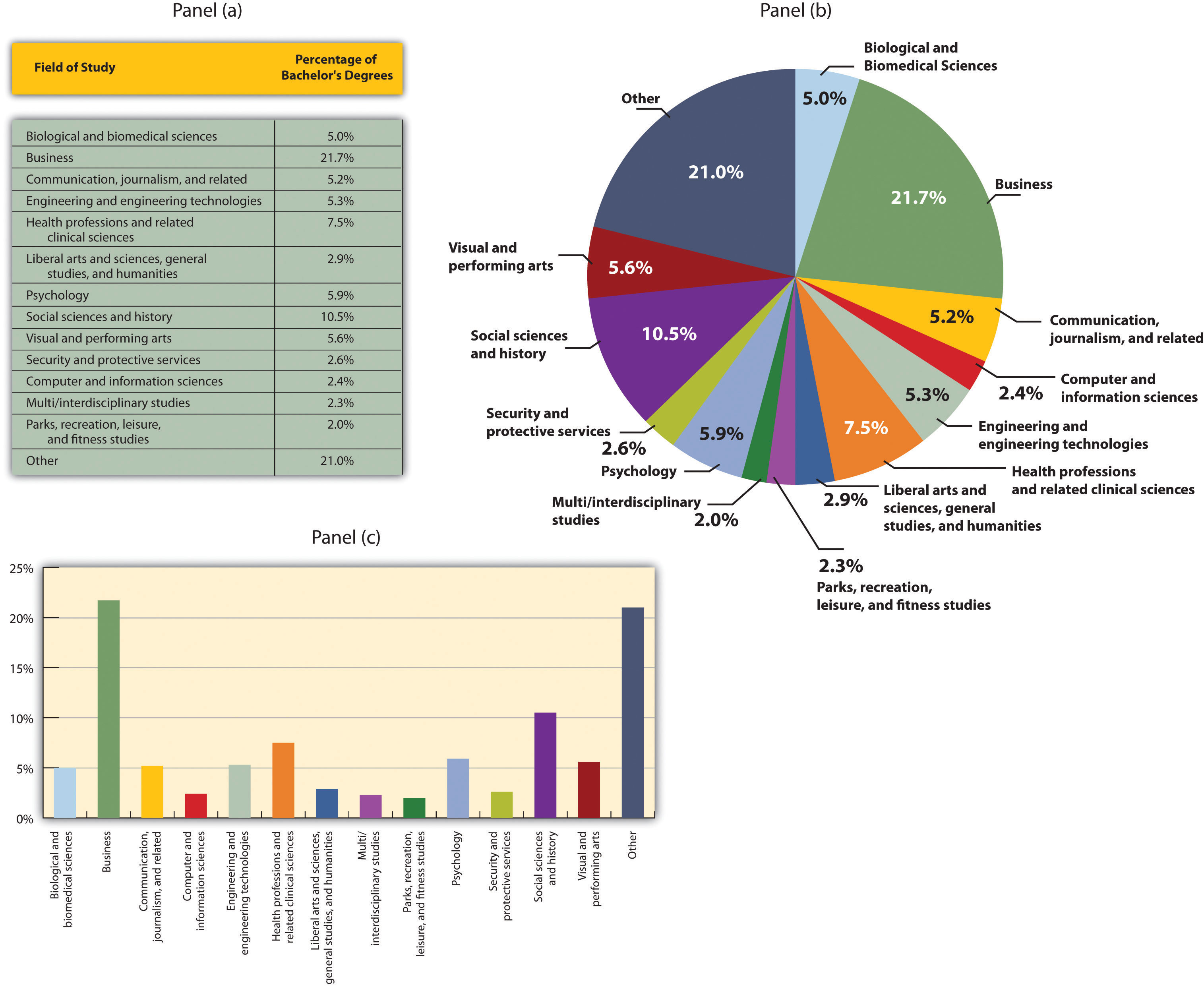
In the introductory geosciences, we use them for: There are many instances in the geosciences where scientists use a best fit line.

#The two data curves on the figure illustrate that download#

You can also download and print a single sheet for constructing a best fit line with the area method (Acrobat (PDF) PRIVATE FILE 33kB Sep10 08) or the dividing method (Acrobat (PDF) PRIVATE FILE 34kB Sep10 08).

Does the data look like a line? or a big blob? Try to approximate the general trend of the data with your mind (even if it's just a blob).

Take a look at the data and as yourself these questions.

Most people start by eye-balling the data. Instead, the idea is to get a line that has equal numbers of points on either side. In many cases, the line may not pass through very many of the plotted points. How do I construct a best-fit line?Ī best-fit line is meant to mimic the trend of the data.

#The two data curves on the figure illustrate that how to#

Work through it and the sample problems if you are unsure of how to complete questions about trends and best-fit lines. This page is designed to help you complete any of these types of questions. You may also be asked to approximate the trend, or sketch in a line that mimics the data. If you find yourself faced with a question that asks you to draw a trend line, linear regression or best-fit line, you are most certainly being asked to draw a line through data points on a scatter plot. All of these applications use best-fit lines on scatter plots (x-y graphs with just data points, no lines). For predictive purposes, we might prefer to know how often an earthquake is likely to occur on a particular fault or the possibility of a very large flood on a given river. We want to know if there is a relationship between the amount of nitrogen in the water and the intensity of an algal bloom, or we wish to know the relationship of one chemical component of a rock to another. In introductory geoscience, most exercises that ask you to construct a best-fit line have to do with wanting to be able recognize relationships among variables on Earth or to predict the behavior of a system (in this case the Earth system).